Hệ số nhị phân là gì?
Máy tính không sử dụng số thập phân (từ 0 đến 9) như chúng ta. Máy tính dùng điện để giao tiếp, tính toán và xử lý. Máy tính chỉ có 2 trạng thái là có điện và không có điện. Vậy làm sao để máy tính có thể lưu trữ, xử lý dữ liệu cho chúng ta kết quả. Chúng ta quy ước có điện tương đương với số 1 và không có điện ứng với số 0. Để hiểu rõ máy tính sẽ làm gì với 2 số này thì trong bài viết sẽ cho các bạn giải đáp.
Số nhị phân là gì?
Số nhị phân được viết dưới dạng số 0 và số 1. Số nhị phân chỉ được tạo thành từ 0 và 1. Ví dụ về số nhị phân: 101001 Không có 2, 3, 4, 5, 6, 7, 8 hoặc 9 trong hệ thống số nhị phân Binary.
Hệ thống số nhị phân, trong toán học, hệ thống số vị trí sử dụng 2 làm cơ số, do đó chỉ yêu cầu hai ký hiệu khác nhau cho các chữ số của nó, 0 và 1, thay vì 10 ký hiệu khác nhau thông thường cần thiết trong hệ số thập phân. Do đó, các số từ 0 đến 10 ở dạng nhị phân 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001 và 1010. Tầm quan trọng của hệ nhị phân đối với lý thuyết thông tin và công nghệ máy tính chủ yếu bắt nguồn từ sự nhỏ gọn và cách thức đáng tin cậy trong đó các số 0 và 1 có thể được biểu diễn trong các thiết bị cơ điện với hai trạng thái — chẳng hạn như “bật-tắt”, “mở” hoặc “không hoạt động”.
Hệ thống số nhị phân là một loại kỹ thuật biểu diễn số. Nó phổ biến nhất và được sử dụng trong các hệ thống kỹ thuật số. Hệ nhị phân được sử dụng để biểu diễn các đại lượng nhị phân có thể được biểu diễn bằng bất kỳ thiết bị nào chỉ có hai trạng thái hoạt động hoặc các điều kiện có thể. Ví dụ, một công tắc chỉ có hai trạng thái: mở hoặc đóng. Trong Hệ thống nhị phân, chỉ có hai ký hiệu hoặc giá trị chữ số có thể có, tức là, 0 và 1. Được biểu diễn bởi bất kỳ thiết bị nào chỉ có 2 trạng thái hoạt động hoặc các điều kiện có thể. Số nhị phân được biểu thị bằng cách thêm tiền tố 0b hoặc hậu tố 2. Vị trí của mọi chữ số có trọng số là lũy thừa của 2. Mỗi vị trí trong hệ nhị phân có ý nghĩa gấp 2 lần so với vị trí trước đó, điều đó có nghĩa là giá trị số của một số nhị phân được xác định bằng cách nhân mỗi chữ số của số đó với giá trị của vị trí mà chữ số xuất hiện và sau đó thêm các sản phẩm. Vì vậy, nó cũng là một hệ thống số vị trí (hoặc trọng số).
| BIT QUAN TRỌNG NHẤT (MSB) | ĐIỂM NHỊ PHÂN | BIT QUAN TRỌNG NHẤT (LSB) | |
| 22 | 21 | 20 | 2-1 2-2 2-3 |
| 4 | 2 | 1 | 0,5 0,25 0,125 |
Ví dụ 1: Số 125 được biểu diễn là:
125 = 1×26+1×25+1×24+1×23+1×22+0x21+1×20=1111101
Ở đây, phần lớn bên phải bit 1 là bit ít quan trọng nhất (LSB) và bên trái nhất bit 1 là bit quan trọng nhất (MSB).
Ví dụ 2: Số 90,75 được biểu diễn là:
90.75 = 1×26+0x25+1×24+1×23+0x22+1×21+0x20+1×2-1+1×2-2=1011010.11
Ở đây, phần lớn bên phải bit 1 là bit ít quan trọng nhất (LSB) và bên trái nhất bit 1 là bit quan trọng nhất (MSB).
Ví dụ 3: Một số thập phân 21 để biểu diễn trong nhị phân là:
(21)10 =16+0+4+0+1 = 1×24+0x23+1×22+0x21+1×20 =(10101)2
Hệ thống số nhị phân rất hữu ích trong công nghệ máy tính và các ngôn ngữ lập trình máy tính cũng sử dụng hệ thống số nhị phân rất hữu ích trong việc mã hóa kỹ thuật số. Hệ thống số nhị phân cũng có thể được sử dụng trong đại số Boolean.
Ưu điểm chính của việc sử dụng hệ nhị phân là nó là một cơ sở dễ dàng được biểu diễn bằng các thiết bị điện tử. Hệ thống số nhị phân cũng dễ sử dụng trong mã hóa, ít tính toán hơn và ít lỗi tính toán hơn. Nhược điểm chính của số nhị phân là khó đọc và viết đối với con người vì số lượng lớn nhị phân của một số thập phân tương đương.
Cách chuyển đổi
Để đổi một số thập phân sang nhị phân, chúng ta lấy số muốn đổi sang nhị phân chia với 2 và sau đó lấy kết quả chia tiếp tục chia với 2, và lập lại phép chia này cho đến khi ta nhận được kết quả là 0 (từ trên xuống, theo mũi tên màu xanh). Ở phép chia này, ta lấy dư là 0 và 1. Sau khi chia đến kết quả bằng 0, ta sẽ lấy các con số dư ghi lại từ dưới lên (theo chiều mũi tên màu đỏ) ta được dãy số gồm 0 và 1, đây chính là giá trị ta cần tìm (các số dư chỉ là 0 và 1, không được chia kết quả ra phần lẻ, ví dụ như 2,5).
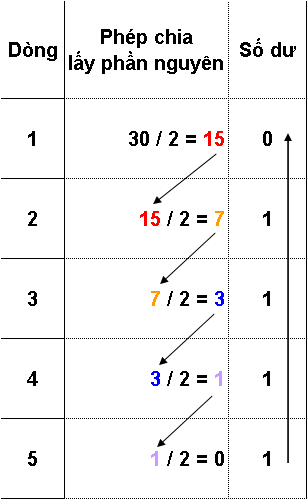
Đổi ngược lại
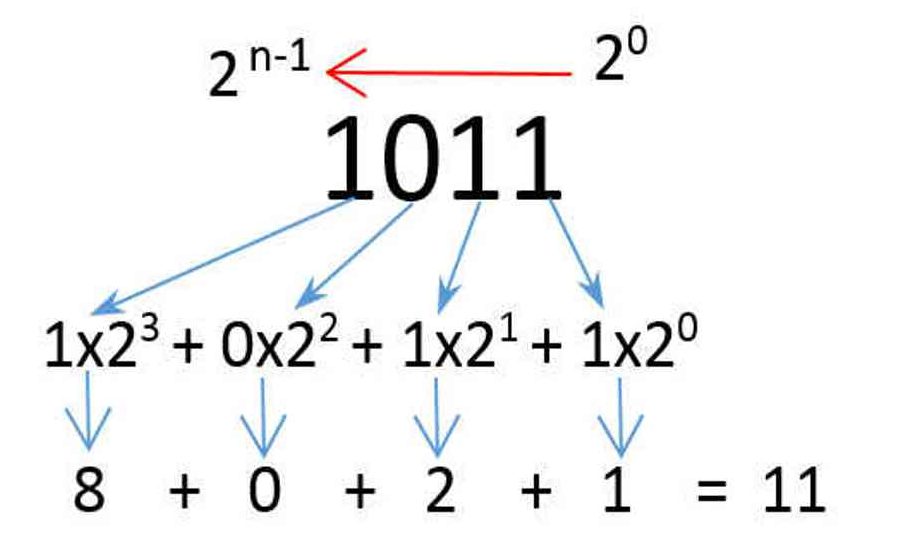
Nguyên tắc cộng 2 số nhị phân:
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10 (nhớ 1 để cộng vào hàng trước nó, tương tự như phép cộng số thập phân).














